High-Pressure Quartz Tube Solution
This article walks through a real case where a high-pressure quartz tube was required for experimental use.
It focuses on how pressure resistance, temperature limits, and practical design questions were assessed to reach a workable solution.
Table of Contents
Background
Customer Background
A graduate student from the Nuclear Engineering Department of a top science and technology university in South Korea, specializing in thermal-hydraulics and energy systems. The experiment requires a high-pressure, high-temperature environment.
Core Requirement
Custom quartz tube: high precision (inner diameter 7.75 mm, tolerance to be confirmed), capable of withstanding high pressure (10 MPa) and high temperature (500 °C).
Implicit Requirements
The quartz tube must be of high purity (to avoid impurities interfering with IR imaging) and may require material certification (e.g., SEMI standards).
Technical Risk Points
Matching the thermal expansion coefficient of the quartz tube with the ITO heater at 500 °C to avoid cracking.
High-pressure CO₂ application may require a gas-tightness test report.
Can a Quartz Tube Withstand 10 MPa Pressure? (Part 1 of 6)
1. Analysis of Quartz Tube Pressure Resistance
The pressure resistance of a quartz tube (fused silica) depends on several factors, including:
- Material purity (higher purity quartz has greater strength)
- Wall thickness (thicker walls offer higher pressure resistance)
- Manufacturing process (seamless tube vs. welded tube)
- Temperature effects (high temperatures reduce mechanical strength)
Typical pressure resistance range for quartz tubes:
- Standard commercial quartz tubes (wall thickness 1–2 mm): typically withstand 1–3 MPa (10–30 bar) static pressure.
- High-pressure quartz tubes (wall thickness 3–5 mm, special annealing process): can withstand 5–10 MPa or more (custom production required).
A pressure of 10 MPa (~100 bar) is considered high pressure. Standard quartz tubes cannot usually meet this requirement directly — thick-walled or specially reinforced tubes are necessary.
2. Key Considerations for 10 MPa Applications
(1) Wall Thickness Calculation (Estimation)
Using the thin-walled cylindrical pressure vessel formula:
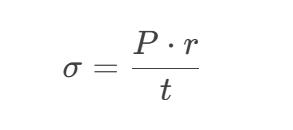
- σ: tensile strength of quartz (~50 MPa, decreases at high temperature)
- P: internal pressure (10 MPa)
- r: inner radius (7.75 mm → radius 3.875 mm)
- t: required minimum wall thickness
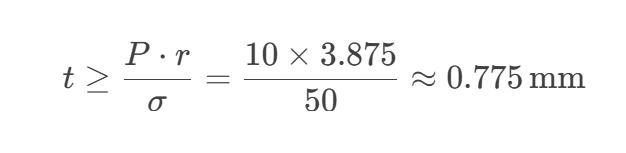
In practice, the following must be considered:
- Safety factor (at least 3–5×, recommended wall thickness ≥3 mm)
- High-temperature strength reduction (at 500 °C, strength may decrease by 30–50%)
Conclusion:
A high-purity quartz tube with wall thickness of at least 3–5 mm is needed to safely withstand 10 MPa pressure.
(2) Other Critical Factors
- End sealing: High pressure requires special flanges or metal encapsulation to prevent port cracking.
- Surface defects: Microcracks or bubbles significantly reduce pressure resistance — optical-grade defect-free quartz is required.
- Cyclic pressure testing: If the experiment involves pressure fluctuations, fatigue life assessment is necessary.
3. Recommended Solutions
(1) Custom High-Pressure Quartz Tube
- Material: High-purity fused silica (SiO₂ > 99.99%) to minimize impurity-related weakening.
- Wall thickness: Recommended ≥3 mm (outer diameter ≈14–15 mm).
- Manufacturing process:
- Seamless drawing (avoid welded weak points)
- Annealing (eliminate internal stress)
- Surface polishing (reduce microcracks)
(2) Alternative Solutions
- Quartz + metal composite tube: Inner quartz layer (corrosion resistance), outer stainless steel layer (pressure bearing), but may affect IR transmission.
- Sapphire tube: Much higher pressure resistance (up to 100 MPa), but cost is extremely high (~10× quartz).
(3) Supplier Communication Points
- Clearly specify working conditions: “10 MPa static pressure + 500 °C high temperature”
- Request pressure test report (e.g., burst pressure ≥30 MPa)
- Confirm end treatment method (threaded, flanged, or O-ring seal)
4. Application Considerations
- High-pressure CO₂ fluid: Ensure no chemical reaction between quartz and CO₂ (generally safe).
- ITO heater compatibility: The 9.53 mm OD heater must be adapted to the thicker quartz tube (custom OD ≈14–15 mm).
- Safety protection: Install safety valves and blast shields to prevent injury from tube rupture.
Conclusion
A standard quartz tube (wall thickness 1–2 mm) cannot meet the 10 MPa high-pressure requirement.
A custom high-pressure quartz tube is required with:
- Wall thickness ≥3 mm (outer diameter ≈14–15 mm)
- High-purity seamless fused silica
- Pressure test certification
It is recommended to contact a specialized quartz manufacturer and specify detailed technical requirements.
The difference between internal pressure resistance and external pressure resistance of quartz tubes (Part 2 of 6)
The pressure resistance of quartz tubes varies depending on whether they are subjected to internal pressure (internal pressure) or external pressure (external pressure), and is mainly influenced by material mechanical properties, structural shape, and failure mode.
Taking the structural shape of inner and outer circles as an example, here are the key differences:
1. Comparison of internal pressure resistance (internal pressure) vs. external pressure resistance (external pressure):
| Characteristics | Internal pressure resistance (internal pressure) | External pressure resistance (external pressure) |
|---|---|---|
| Direction of force | Internal pressure expands outward | External pressure compresses inward |
| Destruction Mode | Tensile rupture (tube wall torn apart) | Buckling instability (tube wall collapse) |
| Key influencing factors | The tensile strength of quartz (~50 MPa) | The compressive strength of quartz (~1100MPa)However, it is limited by geometric stability in practice. |
| Typical voltage withstand value | Standard quartz tube:1~3MPa Thickened/high-pressure tube:5~20MPa | Standard quartz tube:0.1~0.5MPa Thickened/high-pressure tube:1~5MPa |
| Applicable scenarios | High-pressure reactor, fluid delivery pipe | Vacuum environment, external pressure test |
2. Detailed analysis
Failure mechanism: Quartz is a brittle material with low tensile strength (~50MPa). Under high pressure, the pipe wall is subjected to circumferential tensile stress and is prone to cracking at weak points (such as microcracks and bubbles).
The hoop stress formula (thin-wall theory) is expressed as:

Variables Explanation:
σhoop: Hoop stress (MPa)
P: Internal pressure (MPa)
r: Inner radius (mm)
t: Wall thickness (mm)
Key Notes:
Applicability: Valid for thin-walled tubes(t/r≤0.1)
Safety Factor: Actual design stress should include a 3–5x safety margin.
Limitation: Neglects axial stress and end effects.
Example Calculation:
For a tube with
r=5mm, t=1mm, and P=10MPa:

(Compare to quartz’s tensile strength ~50MPa to assess failure risk.)
Reference Standards:
ASME BPVC Section VIII (Pressure Vessels)
ISO 3585 (Fused Quartz Specifications)
Let me know if you need derivations or edge-case adaptations (e.g., thick-wall theory).
If

≥50MPa,the quartz tube may rupture.
Calculation for this case:
Quartz tube with an inner diameter of 7.75 mm and a wall thickness of 1 mm, theoretical pressure resistance:

However, the actual safety pressure is only 1 to 3 MPa (defects and temperature effects must be taken into account).
(2) External Pressure Resistance (Outer Pressure)
Failure Mechanism: While quartz has high compressive strength (~1100 MPa), slender tubes are prone to buckling (similar to a straw being crushed).
Critical Buckling Pressure (Simplified Euler Formula):

E = Elastic modulus of quartz (~72 GPa)
ν = Poisson’s ratio (~0.17)
D = Outer diameter (mm)
t = Wall thickness (mm)
Key Notes:
1.This formula applies to thin-walled tubes under uniform external pressure.
2.Actual safe pressure should apply a safety factor (typically 3–5×).
3.Geometric imperfections (e.g., ovality) significantly reduce P critical
Example: For a tube with D=10mm andt=1mm:
P critical ≈1.5MPa (theoretical),
Practical safe pressure<0.5MPa
Example Calculation:
For a quartz tube with outer diameter = 10 mm and wall thickness = 1 mm, the critical buckling pressure is calculated as:

Note:
The actual safe external pressure is typically < 0.5 MPa (must account for geometric imperfections).
3. Your Application Scenario Analysis
(1) Internal CO₂ High Pressure (10 MPa)
Requirement: Inner diameter 7.75 mm, capable of withstanding 10 MPa.
Issue: Standard quartz tubes (wall thickness 1–2 mm) cannot meet the requirement (theoretically requires ≥3 mm wall thickness).
Solution:
Custom-made thick-walled quartz tubes (e.g., wall thickness 3–5 mm, outer diameter ≈14–17 mm).
Use sapphire tubes (pressure-resistant >100 MPa, but high cost).
Translated with DeepL.com (free version)
4. Conclusion
Internal pressure resistance (internal pressure): Limited by tensile strength, ordinary quartz tubes can withstand pressures of 1 to 3 MPa. For pressures of 10 MPa, thicker tubes must be custom-made.
External pressure resistance (external pressure): Limited by buckling stability, pressure resistance is typically less than 0.5 MPa. External compression must be avoided.
- Your experiment:
- Internal pressure of 10 MPa → High-pressure custom quartz tubes (wall thickness ≥ 3 mm) must be used.
- Considering a heating temperature of 500°C → Compressive strength decreases by 30%–50% at high temperatures → Theoretical wall thickness ≥ 3 mm × 2 = ≥ 6 mm.
- Considering uncertainties in quartz tube purity, processing, and transportation, appropriate redundancy is provided → Redundant thickening of 2 mm (wall thickness ≥ 8 mm).
- External pressure → Ensure that the heater is installed without additional mechanical stress.
It is recommended to purchase high-purity quartz tubes with a purity of no less than 99.9%:
“Inner diameter 7.75 mm, wall thickness ≥ 8 mm, static pressure resistance 10 MPa”
Relationship Between Quartz Tube Wall Thickness and Pressure Resistance (Part 3 of 6)
The pressure resistance of quartz tubes (especially internal pressure, i.e., internal load) is directly related to wall thickness. However, it is not a simple linear proportional relationship, as it is influenced by multiple factors such as material strength, geometric dimensions, and temperature. The key analysis is as follows:
1. Theoretical Calculation Formula (Thin-Walled Cylinder Model)
For internal pressure (internal load), the pressure resistance of quartz tubes can be estimated using the thin-walled pressure vessel formula:
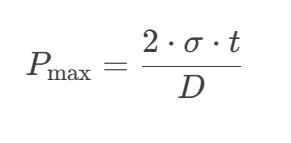
- P = Maximum allowable internal pressure (MPa)
- σ = Tensile strength of quartz (~50 MPa, decreases at high temperature)
- t = Wall thickness (mm)
- D = Inner diameter (mm)
Key Conclusion:
- Pressure resistance P is directly proportional to wall thickness t (greater thickness → higher resistance).
- Pressure resistance P is inversely proportional to inner diameter D (smaller diameter → higher resistance).
Calculation Example
| Inner Diameter D (mm) | Wall Thickness t (mm) | Theoretical Pressure P (MPa) | Actual Safe Pressure (MPa) |
|---|---|---|---|
| 7.75 | 1.0 | 12.9 | 3–5 |
| 7.75 | 2.0 | 25.8 | 6–10 |
| 7.75 | 3.0 | 38.7 | 10–15 |
| 10.0 | 1.0 | 10.0 | 2–4 |
Note: In practical applications, a safety factor (typically 3–5 times) must be considered. Therefore, the rated commercial pressure values of quartz tubes are much lower than the theoretical ones.
2. Actual Relationship Between Wall Thickness and Pressure Resistance
(1) Standard Quartz Tubes (Wall Thickness 1–2 mm):
- Inner diameter 5–10 mm: Typical pressure resistance 1–5 MPa
- Inner diameter >10 mm: Pressure resistance decreases further (e.g., ID 20 mm, WT 2 mm → only ~1 MPa)
(2) High-Pressure Quartz Tubes (Wall Thickness 3–5 mm):
- Inner diameter 5–10 mm: Pressure resistance 10–20 MPa (requires seamless + annealing process)
- Applications: High-pressure chemical reactions, supercritical fluid experiments
(3) Extremely Thick-Walled Tubes (Wall Thickness >5 mm):
- Pressure resistance can exceed 30 MPa, but cost is high, weight increases, and heating uniformity may be affected.
3. Other Key Factors Affecting Pressure Resistance
(1) Temperature:
Quartz tensile strength decreases by about 30%–50% at 500°C, requiring increased wall thickness or reduced working pressure.
(2) Material Defects:
Micro-cracks, bubbles, and other defects significantly reduce actual pressure resistance. Optical-grade, defect-free quartz tubes should be selected.
(3) End Sealing:
Tube ends are prone to rupture under high pressure. Flanges/metal encapsulation should be used for enhanced support.
4. Requirement Verification (Inner Diameter 7.75 mm, 10 MPa)
Minimum Wall Thickness Calculation:
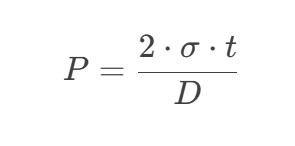
But in practice, the following must be considered:
- Safety factor (3–5 times) → Wall thickness ≥ 2.5–3.0 mm
- High-temperature strength reduction → Recommended wall thickness ≥ 3.5 mm
Recommended Solution:
- Custom quartz tube parameters: ID 7.75 mm, OD ≈14–15 mm (WT ≥ 3.5 mm)
- Material: High-purity fused quartz (SiO₂ > 99.99%)
- Process: Seamless drawing + annealing
5. Conclusion
Wall thickness is directly proportional to pressure resistance, but inner diameter, temperature, and material quality must also be considered.
For high-pressure experiments (10 MPa) with high-purity fused quartz (SiO₂ > 99.99%), without considering temperature fluctuations:
- A wall thickness of ≥3.5 mm must be used.
- Seamless + annealing process should be prioritized, and leak testing must be conducted before delivery.
- If further optimization (weight reduction/cost saving) is needed, sapphire tubes (pressure resistance >100 MPa) or specially designed high-pressure quartz tubes may be considered.
Relationship Between Quartz Tube Wall Thickness and Vacuum Pressure (Part 4 of 6)
The stability of quartz tubes in a vacuum environment is closely related to wall thickness. Unlike internal pressure resistance, vacuum conditions primarily involve the compressive effect of external atmospheric pressure (0.1 MPa) on the tube wall, i.e., the problem of external pressure stability. Below is a detailed analysis:
1. Failure Mechanisms of Quartz Tubes Under Vacuum
Quartz is a brittle material with very high compressive strength (~1100 MPa). However, under vacuum conditions, the main failure modes are:
- Buckling instability: Tube walls are compressed inward by atmospheric pressure, leading to structural collapse (similar to a straw being crushed).
- Microcrack propagation: If there are defects on the quartz surface, vacuum may cause cracks to expand, reducing strength.
Key influencing factors:
- Ratio of wall thickness (t) to outer diameter (D) (t/D)
- Ratio of length (L) to diameter (slenderness ratio)
- Material uniformity (absence of bubbles or microcracks)
2. Theoretical Calculation (Critical Buckling Pressure)
For long cylindrical thin-walled tubes, the critical buckling pressure (Pcr) can be estimated using the Bresse formula:
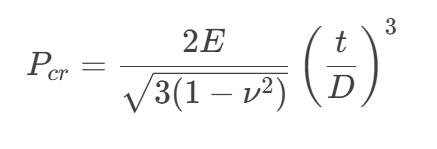
- E = Elastic modulus of quartz (72 GPa)
- ν = Poisson’s ratio (0.17)
- t = Wall thickness (mm)
- D = Outer diameter (mm)
Simplified formula (valid when L/D > 5):
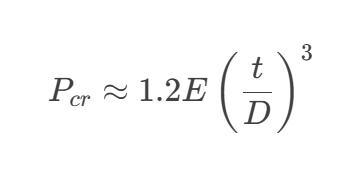
Calculation Examples
| Outer Diameter D (mm) | Wall Thickness t (mm) | t/D | Critical Buckling Pressure Pcr (MPa) | Vacuum Resistant (0.1 MPa)? |
|---|---|---|---|---|
| 10 | 1.0 | 0.1 | 0.086 | ❌ Possibly collapses |
| 10 | 2.0 | 0.2 | 0.691 | ✅ Safe |
| 20 | 1.0 | 0.05 | 0.011 | ❌ Extremely unstable |
| 20 | 3.0 | 0.15 | 0.437 | ✅ Safe |
Conclusion:
When t/D ≥ 0.1 (i.e., wall thickness ≥ 10% of outer diameter), quartz tubes can withstand standard vacuum (0.1 MPa).
For long tubes (L/D > 20), additional wall thickness or support structures (such as internal reinforcement) are required.
3. Practical Application Recommendations
- Safe Wall Thickness Selection
- Short tubes (L < 200 mm): t/D ≥ 0.1 (e.g., outer diameter 10 mm → wall thickness ≥ 1 mm).
- Long tubes (L > 500 mm): t/D ≥ 0.15 (e.g., outer diameter 10 mm → wall thickness ≥ 1.5 mm), or use segmented supports (such as flanges).
- Special Requirements for High Vacuum (<10⁻³ Pa)
- Wall thickness should be further increased (t/D ≥ 0.2) to prevent leakage or gas permeation.
- End sealing: metal flanges with O-rings are recommended instead of adhesives, which may outgas.
- Your Experimental Scenario (1 m tube)
- If outer diameter = 9.53 mm:
Minimum safe wall thickness: t ≥ 0.15 × 9.53 ≈ 1.43 mm → recommendation ≥ 2 mm. - For ultra-high vacuum: select wall thickness ≥ 3 mm, or use quartz tube with stainless steel lining.
- If outer diameter = 9.53 mm:
4. Comparison With Internal Pressure Resistance
| Characteristics | Internal Pressure Resistance | Vacuum Resistance (External Pressure) |
|---|---|---|
| Failure Mode | Tensile rupture (hoop stress) | Buckling collapse (axial compression) |
| Key Formula | F₁ | F₂ |
| Wall Thickness Effect | Linear proportional (P ∝ t) | Cubic relationship (Pcr ∝ t³) |
| Your Requirement | 10 MPa → wall thickness ≥ 3.5 mm | Vacuum → wall thickness ≥ 1.5 mm |
Formula Reference:
- F₁ (Internal Pressure):
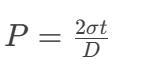
- F₂ (Vacuum Resistance
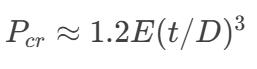
5. Comprehensive Recommendations
- Prioritize high-pressure requirements:
Your experiment requires internal pressure of 10 MPa → wall thickness ≥ 3.5 mm (outer diameter ≈ 14–15 mm).
This wall thickness already exceeds vacuum safety requirements (t/D ≈ 0.25), so no additional reinforcement is needed. - Anti-buckling measures for long tubes:
For tubes ≥ 1 m, use metal flanges at both ends to prevent midsection bending. - Technical communication key points:
Clearly define: “At room temperature, non-corrosive gas, inner diameter 7.75 mm, wall thickness 3.5 mm, resistant to internal pressure 10 MPa + vacuum 0.1 MPa.”
If possible, obtain vacuum leakage rate test data (e.g., <10⁻⁹ Pa·m³/s).
Conclusion
- Vacuum resistance and wall thickness have a cubic relationship. Even a small increase in wall thickness significantly improves stability.
- Our design (wall thickness 3.5 mm) meets both high-pressure and vacuum requirements, provided the end sealing is reliable.
- If there are other technical details not mentioned, they must be clarified, as any missing key data will directly affect quartz tube design and experimental outcomes.
Relationship Between Quartz Tube Diameter and Pressure Resistance (Part 5 of 6)
1. Core Relationship (Thin-Wall Theory Formula)
The maximum allowable internal pressure (Pmax) of a quartz tube is inversely proportional to its inner diameter (D).
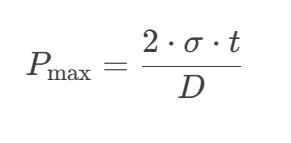
Formula:
- Pmax = Maximum internal pressure (MPa)
- σ = Tensile strength of quartz (~50 MPa, decreases at high temperatures)
- t = Wall thickness (mm)
- D = Inner diameter (mm)
Key Conclusion: Pressure resistance is inversely proportional to the inner diameter.
- Smaller inner diameter → higher pressure resistance (at the same wall thickness).
- Larger inner diameter → significantly reduced pressure resistance.
2. Pressure Resistance Comparison for Different Inner Diameters (Fixed Wall Thickness = 2 mm)
| Inner Diameter D (mm) | Theoretical Pressure (MPa) | Practical Safe Pressure (MPa) |
|---|---|---|
| 5 | 40 | 8–12 |
| 10 | 20 | 4–6 |
| 20 | 10 | 2–3 |
| 50 | 4 | 0.8–1.2 |
Note: In real applications, a safety factor of 3–5 is required. Therefore, the rated working pressure is always lower than the theoretical value.
3. Combined Influence of Diameter and Wall Thickness
- Small Diameter Tubes (D < 10 mm):
- Advantage: Naturally high pressure resistance, suitable for high-pressure experiments (e.g., microreactors, capillary fluid systems).
- Example: ID 5 mm, wall thickness 2 mm → working pressure 8–12 MPa.
- Large Diameter Tubes (D > 20 mm):
- Disadvantage: Rapid decline in pressure resistance, requiring much greater wall thickness.
- Example: ID 50 mm, wall thickness 5 mm → only ~2 MPa.
- To withstand 10 MPa, wall thickness ≥25 mm would be needed (impractical; recommend alumina or sapphire tubes instead).
4. Application Case: ID 7.75 mm, 10 MPa Requirement
- Theoretical minimum wall thickness: 0.775 mm.
- Practical requirement with safety factor: ≥3 mm.
- Outer diameter: 7.75 mm + 2 × 3 mm = 13.75 mm.
Conclusion:
- At ID 7.75 mm with 3 mm wall thickness, 10 MPa pressure is achievable.
- If ID increases to 15 mm with the same wall thickness, the pressure resistance drops to ~5 MPa.
5. Engineering Recommendations for Diameter Selection
- High-Pressure Applications:
- Use small inner diameters (5–10 mm) to minimize wall thickness requirements.
- Large Flow Applications:
- If large diameters (>20 mm) are required, switch to alumina or sapphire tubes.
- Vacuum Applications:
- Large diameters are more prone to buckling and require increased wall thickness or external support.
6. Extreme Case Comparisons
| Inner Diameter D | Wall Thickness t | Theoretical Pressure | Practical Limitation |
|---|---|---|---|
| 1 mm | 1 mm | 100 MPa | Microfluidics feasible, but machining difficult |
| 10 mm | 1 mm | 10 MPa | Safe limit only 2–3 MPa |
| 100 mm | 10 mm | 1 MPa | Only for low-pressure/static use |
7. Final Conclusion
- Diameter is the key variable: halving the inner diameter doubles the pressure resistance (at constant wall thickness).
- For ID 7.75 mm, wall thickness 3 mm is a practical balance, ensuring safe operation at 10 MPa.
- Large diameters (>20 mm) make high pressure impractical, so alumina or sapphire tubes should be considered.
- For optimization, consider wall thickness, material purity, and end-sealing methods together.
High-Pessure Quartz Tube Sealing Solutions (Part 6 of 6)
When quartz tubes are required to operate in high-pressure environments of 10 MPa or above, end-sealing becomes a critical technical challenge. As quartz is a brittle material, traditional adhesive or rubber seals are prone to failure. Instead, metal-quartz composite sealing structures must be used. Below are five engineering solutions for high-pressure sealing.
Solution 1: Metal Flange + Conical Compression Seal
Structural Features:
- Quartz tube ends are machined into a 20° conical surface.
- Stainless steel flanges with matching internal cones.
- Axial pressure applied using hydraulic pre-tightening bolts.
Key Parameters:
- Sealing pressure: ≤30 MPa
- Applicable temperature: −200 °C to 500 °C
- Leak rate: <10⁻⁹ Pa·m³/s
- Annealed quartz tubes required (to prevent stress-concentration cracking).
Advantages: Detachable; suitable for frequent opening and closing during experiments.
Disadvantages: Requires precision machining (cone angle tolerance ±0.5°).
Solution 2: High-Temperature Glass Welding
Process Highlights:
- Fill the gap between quartz tube and metal flange with borosilicate glass powder.
- Melted and welded in a nitrogen environment at 850 °C.
- Slow cooling and annealing to eliminate stress.
Performance Indicators:
- Pressure resistance: 15 MPa (static).
- Temperature resistance: ≤450 °C (glass softens above this point).
- Must use Kovar flanges to match thermal expansion coefficients.
Application: Suitable for permanent sealing, such as in sensor packaging.
Solution 3: Hydraulic Cold Press Sealing
Innovative Process:
- Use ultra-high-pressure molds (1–3 GPa) at room temperature.
- Achieve plastic deformation interlocking between quartz and metal.
- No intermediate solder or adhesives required.
Breakthrough Parameters:
- Pressure resistance: up to 100 MPa (world record).
- Temperature range: −273 °C to 1000 °C.
- Limited to short tubes with wall thickness ≥5 mm.
Solution 4: O-Ring Dynamic Sealing
Special Design:
- FFKM (perfluoroelastomer) O-rings are used.
- Dual-stage pressurization structure:
- Primary seal: 5 MPa hydraulic pre-tightening.
- Secondary seal: metal bellows compensation.
Application Scenarios:
- Systems requiring frequent disassembly and reassembly.
- Maximum pressure: 12 MPa (short-term peak of 15 MPa).
Note: High assembly cost and requires skilled technicians.
Solution 5: Integrated Metallized Sintering
Military-Grade Solution:
- Vacuum sputter multi-layer Ti-Pt-Au coating on quartz tube ends.
- High-temperature sintering to form a metalized transition layer.
- Laser welding to stainless steel flanges.
Performance Limits:
- Burst pressure: up to 50 MPa.
- Thermal shock resistance: withstands 1000 °C → liquid nitrogen cycles without failure.
- Only applicable to thick-walled tubes with ID <20 mm.
Solution Comparison Table
| Solution | Pressure Resistance (MPa) | Temperature (°C) | Detachable | Applicable Tube Diameter | Cost |
|---|---|---|---|---|---|
| Metal Flange | 30 | 500 | ✓ | 5–100 mm | Moderate |
| Glass Welding | 15 | 450 | ✗ | 3–50 mm | Low |
| Cold Press | 100 | 1000 | ✗ | 3–20 mm | Very High |
| O-Ring | 12 | 300 | ✓ | 10–200 mm | High |
| Metallization | 50 | 1000 | ✗ | 3–20 mm | Very High |
Recommended Solution for Your Application
Operating Conditions:
ID = 7.75 mm, Pressure = 10 MPa, Medium = CO₂, Temperature = 500 °C
- Preferred Solution: Solution 1 (Metal Flange + Conical Seal)
Recommended materials: Inconel 718 flange + red copper gasket.
Pre-tightening force: ≥8 tons (M6 bolts × 8 pcs). - Alternative: Solution 5 (if budget allows and disassembly is not required).
- Prohibited: Regular epoxy or silicone adhesives (will fail above 5 MPa).
Implementation Considerations
1. Stress Concentration Control
- Flange contact surfaces must be machined with R0.3 mm rounded transitions.
- Quartz tube ends must be flame-polished.
(Not applicable for thick-walled tubes; polishing may reduce pressure resistance.)
2. Leak Detection Standards
- Helium mass spectrometry leak detection ≤1×10⁻⁸ mbar·L/s.
- Pressure-holding test: maintain 15 MPa for 1 hour, pressure drop <1%.
3. Safety Precautions
- Install explosion-proof shields (recommend 6 mm polycarbonate).
- Real-time pressure sensors + automatic relief valves are required.
For custom engineering sealing solutions under specific experimental conditions, CAD drawings or detailed process specifications (temperature, internal/external pressure, test gases, etc.) are required for further discussion.





